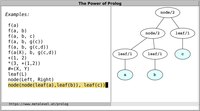
Prolog Data Structures



Terms

In Prolog, all data are represented by Prolog terms.

Video: Terms


Each term is either a variable, an atomic term or a compound term: All data can be represented in this way. Terms come into existence by simply writing them down.

A term is called ground if it contains no variables. A compound term is called partially instantiated if one of its subterms is a variable.

Prolog is dynamically typed and allows us great freedom for representing data. For example, we could represent natural numbers as follows: In this representation, the term s(s(s(zero))) represents the number 3. Such a representation is of course highly impractical due to its enormous size for large numbers. For this reason, Prolog provides integer arithmetic with a much more efficient number representation.

Prolog terms naturally correspond to trees. There is a standard order on terms.

You can define custom prefix-, infix- and postfix operators that let you write terms in different ways.

Video: Operators


Several standard operators are predefined. For example, you can write a+b and X=Y instead of +(a,b) and =(X,Y), respectively.

Lists

Prolog lists are a special case of terms.

Video: Lists


Lists are defined inductively: There is a special syntax for denoting lists conveniently in Prolog:
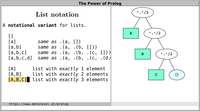
  1. The list '.'(a, '.'(b, '.'(c, []))) can also be written as [a,b,c].
  2. The term '.'(L, Ls) can also be written as [L|Ls].
These notations can be combined in any way. For example, the term [a,b|Ls] is a list iff Ls is a list.

Lists naturally represent collections of elements and arise in almost all Prolog programs. When choosing between lists and any other way to represent collections of elements, ask yourself the following questions: If your answer is "yes" to most of these questions, lists are often a good fit.

In contrast, consider for example the case where each collection comprises exactly three elements. You can use lists of the form [A,B,C] to represent such collections, and thus benefit from meta-predicates that reason over lists. On the other hand, using compound terms of the form f(A,B,C) is more memory efficient: This is because the list [A,B,C] is the compound term '.'(A,'.'(B,'.'(C,[]))) and thus takes roughly twice the space of the term f(A,B,C) in memory.

DCG notation is frequently used for describing lists.

Pairs

Pairs are terms with principal functor (-)/2. For example, the term -(A, B) denotes the pair of elements A and B. In Prolog, (-)/2 is defined as an infix operator. Therefore, the term can be written equivalently as A-B.

Video: Pairs


The standard predicate keysort/2 is an example of a predicate that reasons about pairs. They are called Key-Value pairs because the first argument of each pair is used as the key for sorting. Many Prolog systems provide additional predicates for reasoning about pairs, and they often adopt this terminology from keysort/2. Common examples of such predicates are pairs_keys_values/3 and pairs_keys/2 to relate a list of pairs to their respective keys and values.

Association lists

In many Prolog systems, association lists are available to allow faster than linear access to a collection of elements. These association lists are typically based on balanced trees like AVL trees.

There is a public domain library called library(assoc) that ships with many Prolog systems and provides operations for inserting, fetching and changing elements of a collection.

Here is one way to represent an AVL tree in Prolog:
  1. the empty tree is represented by the atom t.
  2. an inner node is represented as a compound term of the form t(Key, Value, Balance, Left, Right) where:
Every operation on AVL trees, such as adding or changing an association, can be described as a relation between different trees, one tree before the operation and one after it. See Thinking in States for more information.

AVL trees let us perform many important operations in O(log(N)) time, where N is the number of associations. This is acceptably efficient in many cases.

Strings?

Almost everything that needs to be said about strings has been brilliantly said by Richard O'Keefe in his Prolog Library Proposal. In particular, strings are wrong, and:
For almost any use case that involves some kind of processing, the only sensible thing to do with string data is to turn it into some kind of tree early. Prolog is brilliant with trees.
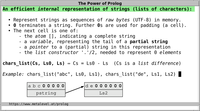
In Prolog, a convenient and natural representation of strings is to use lists of characters, which are one-character atoms. If you set the Prolog flag double_quotes to chars, then double-quoted strings are automatically interpreted as lists of characters. To enable this setting, add the following directive at the start of your Prolog programs, or to your Prolog system's configuration file: 

:- set_prolog_flag(double_quotes, chars).


With this setting, we obtain for example: 
?- "abc" = [a,b,c].
   true.
Thus, working with strings is reduced to working with lists, which can be easily handled in Prolog and are amenable to built-in mechanisms such as DCGs.

Treating strings as lists of characters has a long tradition in Prolog systems, starting with the very first Prolog system, Marseille Prolog. Some Prolog systems opted to represent strings as lists of character codes, i.e., as lists of integers instead of lists of atoms, and these integers represent code points that depend on the used encoding. This behaviour is available if you set the Prolog flag double_quotes to codes. This is not recommended though, because it renders answers much less readable than using chars. Alternatively, you can also set the flag to atom, which makes Prolog treat double-quoted strings as atoms. The main drawback of using the value atom is that atoms preclude the use of DCGs and other predicates that reason about lists and partial lists. In addition, since atoms cannot be partially instantiated, your code will become moded: This means that it can only be used in a proper subset of all conceivable directions.

For these reasons, chars is the recommended setting, and newer Prolog systems such as Scryer, Tau and Trealla Prolog already use this value by default.

With a suitable implementation technique, Prolog systems can represent lists of characters very efficiently, making them both convenient and fast to work with.

Video: Representing Strings


There is thus hope that more Prolog systems will use chars as the default value in the future.

Arrays?

What about arrays? Is there any data structure in Prolog to represent a collection of terms, allowing for O(1) access to individual elements?

First of all, the concept of destructive modifications is alien to logic programming. In Prolog, we describe relations between entities, not destructive effects. To express a change in a Prolog data structure, we define a predicate that relates the state of the structure before the change to a different structure after the change. For this reason, pure modifications often entail some copying of data and typically lead to at least logarithmic overhead (for example, to copy a subtree of a balanced tree).

That being said, we can access the arguments of a term in O(1) with the built-in predicate arg/3. There even is an impure predicate called setarg/3 which allows destructive modifications to a term. Use it at your own peril: If you use setarg/3, you can no longer reason about your code in the way you expect from pure relations. If you really need efficient destructive modifications of terms, it is better to use attributed variables.

Type tests

There are predicates to test for specific types of terms.

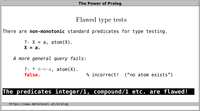
Unfortunately, the standard predicates for type testing (atom/1, integer/1, compound/1 etc.) are logically flawed because they are not monotonic: If you use these predicates, then generalizing a query may lead to fewer solutions, preventing declarative debugging based on logical properties. For example, atom/1 fails for the most general query, even though it succeeds for more specific queries: 
?-        atom(X).
   false.

?- X = a, atom(X).
   X = a.
Therefore, new families of predicates for type testing are now becoming available. They implement type tests with desirable logical properties:

Video: Type tests


The predicates must_be/2 and can_be/2 are especially useful for Prolog library authors. The ..._si/1 family of type tests are useful in normal Prolog programs, if you want to explicitly test for specific types without raising type errors.

Importantly, all these predicates raise instantiation errors if the terms that are tested are not sufficiently instantianted to allow a sound decision.

Clean vs. defaulty representations

When representing data with Prolog terms, ask yourself the following question:
Can I distinguish the kind of each component from its principal functor?
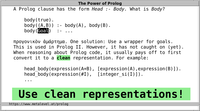
If this holds, your representation is called clean. If you cannot distinguish the elements by their principal functor, your representation is called defaulty, a wordplay combining "default" and "faulty". This is because reasoning about your data will need a "default case", which is applied if everything else fails. In addition, such a representation prevents argument indexing, and is considered faulty due to this shortcoming. Always aim to avoid defaulty representations! Aim for cleaner representations instead.

Video: Clean vs. Defaulty Representations


For example, suppose you represent a full binary tree in Prolog. There are two kinds of elements in a full binary tree: We can represent such trees with Prolog terms as follows: The above is a clean representation: It lets us distinguish the kinds of elements by their principal functor. We can reason about such trees in a way that keeps the code very general and usable in all directions. Such a representation is also amenable to argument indexing.

You can also recognize a clean representation if it lets you describe the general structure of your data while retaining enough flexibility to keep the concrete elements unspecified. For example, in the case of full binary trees, we can represent the general outline of all trees with exactly two leaves as node(leaf(_),leaf(_)). If you had chosen to omit the leaf/1 wrapper for representing leaves, this would become node(_,_): a defaulty representation that no longer represents precisely such manifestations.

Sometimes, it will appear to you that there is no clean way out. For instance, you may be faced with a representation that requires you to distinguish different cases in an impure and non-monotonic way, such as by testing the instantiation of certain arguments via var/1. In such cases, it is good practice to restrict the impure parts of your program to small fragments, and to convert any defaulty representation to a clean one by introducing suitable wrappers that let you distinguish the cases by pattern matching. This helps to ensure that you can use your core predicates in multiple directions.

Term inspection

In Prolog, the most natural way to reason about terms is to rely on unification. In addition, there are several predicates that let you decompose and analyze terms. The most important of these term inspection predicates are functor/3, arg/3 and (=..)/2.

Here are examples that illustrate their usage: 
?- functor(f(a,g(X)), Functor, Arity).
   Functor = f, Arity = 2.

?- functor(Term, f, 2).
   Term = f(_A,_B).

?- arg(2, f(a,g(X)), Arg).
   Arg = g(X).

?- f(a,g(X)) =.. [Functor|Args].
   Functor = f, Args = [a,g(X)].

?- Term =.. [f,a,g(X)].
   Term = f(a,g(X)).
These predicates cannot be defined by a finite set of clauses, and can therefore be considered higher-order predicates. Do not get carried away with these predicates! Everything that can be expressed by pattern matching should be expressed by pattern matching. For example, instead of functor(Term, f, 2), you can simply write Term = f(_,_).

Every Prolog term has a canonical representation. If you are ever unsure about the structure of a term, use write_canonical/1 to obtain the canonical representation. For example: 
?- write_canonical(a+b=[x,y,z]).
=(+(a,b),'.'(x,'.'(y,'.'(z,[]))))
The canonical representation shows the structure of the term in such a way that it can also be easily parsed by external programs.


More about Prolog


Main page