Prolog DCG Primer

Introduction

A Prolog definite clause grammar (DCG) describes a sequence. Operationally, DCGs can be used to parse, generate, complete and check sequences manifested as lists.

Video:

DCGs are of great significance for Prolog: From a historical perspective, Prolog originated from systems that were designed for natural language processing, and a built-in mechanism for efficient parsing that also preserves Prolog's logical characteristics was one of the most important milestones in its development. From a practical perspective, DCGs are frequently used to describe lists because they are so convenient to use.

A DCG is defined by rules. A DCG rule has the form:

Head --> Body.

A rule's body consists of terminal, nonterminals, and grammar goals. A terminal is a list, and stands for the elements it contains. These elements are terminal symbols of the grammar. A nonterminal refers to a DCG or other grammar construct, and stands for the elements it describes. A nonterminal therefore stands for a sequence of terminal symbols. A grammar goal is written in curly brackets as { Goal } and is used to invoke Prolog goals within a grammar. We use the nonterminal indicator A//N to refer to the nonterminal A with arity N. Note that // distinguishes it from a Prolog predicate indicator.

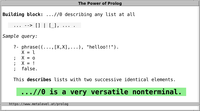
As an example of a DCG, let us describe sequences whose every element is the atom a. We shall use the nonterminal as//0 to refer to such sequences:

as --> [].
as --> [a], as.

The first rule states: The empty sequence is such a sequence. The second rule uses the nonterminal (',')//2, which we read as "and then". Therefore, the second rule states: A sequence that contains as its first element the atom a and then only atoms a is also such a sequence.

To invoke a grammar rule, we use Prolog's built-in phrase/2 predicate. The first argument is, syntactically, a DCG body. phrase(Body, Ls) is true iff Body describes the list Ls.

For example, let us use the single nonterminal as//0 to ask for all lists that it describes, by posting the most general query:

?- phrase(as, Ls).
   Ls = []
;  Ls = [a]
;  Ls = [a,a]
;  Ls = [a,a,a]
;  Ls = [a,a,a,a]
;  ... .

Prolog lets us write lists of characters, i.e., strings, very conveniently if the Prolog flag double_quotes is set to chars, for example by posting the query:

?- set_prolog_flag(double_quotes, chars).
   true.

or by adding the following directive in your initialisation file or program:

:- set_prolog_flag(double_quotes, chars).

We strongly recommend using this setting for better readability of programs, queries and answers. In Scryer Prolog and Tau Prolog, this is already the default setting.

With double_quotes set to chars, the list of characters [a,a,a] can be written equivalently as "aaa", and a Prolog system may therefore report the solutions above equivalently and more compactly as:

?- phrase(as, Ls).
   Ls = []
;  Ls = "a"
;  Ls = "aa"
;  Ls = "aaa"
;  Ls = "aaaa"
;  ... .

Throughout this text, we assume that the Prolog flag double_quotes is set to chars.

Examples of more specific queries and the system's answers:

?- phrase(as, "aaa").
   true
;  false.

?- phrase(as, "bcd").
   false.

?- phrase(as, [a,X,a]).
   X = a
;  false.

Describing sequences with `seq//1`, `seqq//1` and `... //0`

Let us define the nonterminal seq//1 to describe a sequence of elements. We use its single argument to refer to the sequence that it describes, represented as a list:

seq([])     --> [].
seq([E|Es]) --> [E], seq(Es).

Sample use case:

?- phrase(("Hello, ",seq(Cs),"!"), "Hello, all!").
   Cs = "all"
;  false.

Note that in cases where we use DCGs only to generate lists, you might be tempted to define seq//1 as follows:

badseq(Ls) --> Ls.

This still works as expected in cases like:

?- phrase(badseq("abc"), Ls).
   Ls = "abc".

However, it is still not a good idea for two reasons: First, it cannot be used in the other direction and is thus not a pure relation:

?- phrase(badseq(Ls), "abc").
   error(instantiation_error,phrase/3).

Second, such a simplistic definition can be tricked into invoking arbitrary code by specifying {Goal} as the argument, as in:

?- phrase(badseq({halt}), _).

For these two reasons, it is better to use the definition of seq//1 shown above to refer to arbitrary lists with DCGs.

Using seq//1, we can define seqq//1 to describe a sequence of sequences:

seqq([]) --> [].
seqq([Es|Ess]) -->
        seq(Es),
        seqq(Ess).

Sample use:

?- phrase(seqq(["ab","cd","ef"]), Ls).
   Ls = "abcdef".

This is an elegant way to describe the concatenation of arbitrarily many lists.

It is sometimes useful to describe "any sequence at all", and we can do this with the nonterminal ... //0 which is equivalent to seq(_):

... --> [] | [_], ... .

The grammar construct ('|')//2 and its equivalent (;)//2 correspond to the Prolog control structure (;)/2 and are read as "or". When parsing with DCGs, using ('|')/2 is preferable over (;)//2 due to existing conventions for writing grammars.

seq//1, seqq//1 and ... //0 are very versatile nonterminals and can be used to elegantly solve many tasks that involve reasoning over lists. For example, the last element of a list can be described with:

?- phrase((...,[Last]), "hello").
   Last = o
;  false.

As another example, consecutively repeated elements in a list can be described with:

?- phrase((...,[E,E],...), Ls).
   Ls = [E,E]
;  Ls = [E,E,_A]
;  Ls = [E,E,_A,_B]
;  Ls = [E,E,_A,_B,_C]
;  ... .

Using iterative deepening, we obtain a fair enumeration of answers:

?- length(Ls, _), phrase((...,[E,E],...), Ls).
   Ls = [E,E]
;  Ls = [E,E,_A]
;  Ls = [_A,E,E]
;  Ls = [E,E,_A,_B]
;  Ls = [_A,E,E,_B]
;  Ls = [_A,_B,E,E]
;  ... .

In Scryer Prolog, seq//1, seqq//1 and ... //0 are provided by library(dcgs).

List reversal, palindromes and other exercises

When reasoning about lists or solving exercises involving lists, consider using DCGs for convenience.

Video:

For example, the reversal of a list can be described with:

reversal([]) --> [].
reversal([L|Ls]) --> reversal(Ls), [L].

Sample query and answer:

?- phrase(reversal("abcd"), Ls).
   Ls = "dcba".

As another example, a palindrome can be described with:

palindrome --> [].
palindrome --> [_].
palindrome --> [E], palindrome, [E].

This definition can be used to generate, to complete and to check palindromes. For example:

?- phrase(palindrome, "hellolleh").
   true
;  false.


?- phrase(palindrome, Ls).
   Ls = []
;  Ls = [_A]
;  Ls = [_A,_A]
;  Ls = [_A,_B,_A]
;  Ls = [_A,_B,_B,_A]
;  ... .

Challenge: Define palindrome//0 using reversal//1. Provide two different definitions.

Relating trees to lists

Let us now use a DCG to relate a binary tree to the in-order sequence of its node names. Let us assume a binary tree consists of leaves represented by the atom nil and inner nodes of the form node(Name, Left, Right), where Left and Right are themselves binary trees. To obtain the in-order sequence of node names, consider:

tree_nodes(nil) --> [].
tree_nodes(node(Name, Left, Right)) -->
        tree_nodes(Left),
        [Name],
        tree_nodes(Right).

Example:

?- phrase(tree_nodes(node(a, node(b, nil,
                                     node(c, nil, nil)),
                             node(d, nil, nil))), Ns).
   Ns = "bcad".

You can obtain other orders by moving the terminal [Name] in the DCG body.

Left recursion

Conversely, given a sequence of node names, what are the trees that yield this sequence:

?- phrase(tree_nodes(Tree), "abcd").
   Tree = node(a,nil,node(b,nil,node(c,nil,node(d,nil,nil))))
;  % (nontermination)

The system yields one (correct) solution, then loops. This is because the grammar is left-recursive: We recursively refer to a nonterminal (tree_nodes//1) before anything else. To be able to use this grammar for finding all matching trees, we need to encode that for the second rule to apply, at least one list element must be available since the rule contains exactly one terminal, and we need to check this in advance to avoid unbounded recursion. We can do this by introducing two additional arguments that let us limit the number of rule applications to the given list's length:

tree_nodes(nil, Ls, Ls) --> [].
tree_nodes(node(Name, Left, Right), [_|Ls0], Ls) -->
        tree_nodes(Left, Ls0, Ls1),
        [Name],
        tree_nodes(Right, Ls1, Ls).

Each respective pair of additional arguments describes a so-called list difference. To understand this method and its associated terminology, consider for example the pair Ls0 and Ls1. We can interpret the difference of these lists as describing the list of elements that are consumed by the first recursive invocation of tree_nodes//3 in this example. Analogously, the difference of the lists Ls1 and Ls is the list of elements consumed by the second invocation. And the difference between the lists that occur in the head, i.e., that of [_|Ls0] and Ls, describes the list of elements that are consumed by the entire second rule.

Video:

Of course, difference is to be understood in a symbolic sense in these cases, not in an arithmetic sense. For example, the difference between the lists [A,B,C] and [C] is [A,B], the difference between [X,Y|Ls] and Ls is [X,Y], and the difference between Ls and Ls is []. By reasoning about such list differences via argument pairs, we can compose and decompose entire lists by reasoning about their sublists. This powerful method is in fact also the key idea that underlies the common transformation of DCGs to Prolog predicates. In cases where you are using it, consider using DCGs instead. In the present case, we are using list differences explicitly because we are using them within DCGs.

In the literature, you will also encounter the term "difference list". However, this terminology is misleading: We are not talking about—as the name may suggest—a special kind of list. The additional arguments are completely ordinary lists or partial lists. It is their differences that matter especially in such cases.

When working with list differences, you may be tempted to pass around each pair as a single argument, for example as compound terms like Ls0-Ls1 or Ls0/Ls1. However, this is not advisable, primarily because you will likely run into conflicts with other predicates and DCG expansions, and secondarily because it incurs performance overhead for constructing, decomposing and managing these compound terms.

Example query:

?- Ns = "abcd", phrase(tree_nodes(Tree, Ns, _), Ns).
   Ns = "abcd", Tree = node(a,nil,node(b,nil,node(c,nil,node(d,nil,nil))))
;  Ns = "abcd", Tree = node(a,nil,node(b,nil,node(d,node(c,nil,nil),nil)))
;  Ns = "abcd", Tree = node(a,nil,node(c,node(b,nil,nil),node(d,nil,nil)))
;  ... .

Another option to parse with left-recursive grammars is to use your Prolog system's tabling mechanism. Combining tabled execution with DCGs yields packrat parsing; an interesting paper about this topic is DCGs + Memoing = Packrat Parsing, But is it worth it? by Ralph Becket and Zoltan Somogyi.

Semicontext notation

Using semicontext notation, in now outdated terminology also called pushback lists or right-hand context, we can make statements about remaining elements. Operationally speaking, we can insert list elements that were initially not in the list that is being parsed. A DCG rule of the form:

Head, [T₁,...,T_n] --> Body.

can be read operationally as: parse the list using Body, then prepend the terms T₁, ..., T_n to the remaining list. For example:

nt1, [b] --> [a].
nt2      --> [b].

The body of nt1//0 describes a list whose single element is the atom a. Operationally, after nt1//0 has consumed the atom a in a list that is being parsed, it inserts the atom b in front of the remaining list. nt2//0 describes a list whose single element is the atom b. The following query therefore succeeds, since nt2//0 consumes the atom b, which is left in the list after nt1//0 succeeds:

?- phrase((nt1,nt2), "a").
   true.

We can also use nt1//0 in isolation. However, the following query fails since phrase/2 only succeeds if all list elements are consumed by the given DCG body:

?- phrase(nt1, "a").
   false.

The list difference version phrase/3 shows what remains after nt1//0 succeeds:

?- phrase(nt1, "a", Rest).
   Rest = "b".

As expected, the atom b remains in the list.

Using semicontext notation, we can implement look ahead, which lets us inspect the next element in the list without removing it. Operationally, we first remove it and then push it back:

look_ahead(T), [T] --> [T].

Example:

?- phrase(look_ahead(T), "a", Rest).
   Rest = "a", T = a.

Implicitly passing states around

Semicontext notation is also useful to implicitly pass around a state representation that is only accessed and changed by a subset of rules. For example, let us count the leaves in a binary tree with the above presentation. Without using DCGs, we can relate a tree to the number of its leaves as follows:

num_leaves(Tree, N) :-
        num_leaves_(Tree, 0, N).

num_leaves_(nil, N0, N) :- N #= N0 + 1.
num_leaves_(node(_,Left,Right), N0, N) :-
        num_leaves_(Left, N0, N1),
        num_leaves_(Right, N1, N).

Notice that in the second clause of num_leaves_/3, the accumulator is only passed through as N0, N1, ..., N and not modified directly. When you encounter such a pattern, consider using DCG notation to pass around the arguments implicitly. In this concrete case, the state we shall pass around is a single integer denoting the number of leaves encountered so far. To increment the state, we use Prolog's declarative integer arithmetic like above. To invoke a Prolog predicate from within a DCG body, we use the DCG language construct {}//1. Operationally, when the construct {Goal} is encountered in a DCG body, Goal is called as a Prolog goal. Since a DCG must always describe a list, we wrap the state into a list and thus describe a list containing a single element. The initial state is again sensibly specified as 0, and the number of leaves is given by the remaining list element after num_leaves_//1 succeeds:

num_leaves(Tree, N) :-
        phrase(num_leaves_(Tree), [0], [N]).

num_leaves_(nil), [N] --> [N0], { N #= N0 + 1 }.
num_leaves_(node(_,Left,Right)) -->
        num_leaves_(Left),
        num_leaves_(Right).

Notice that the second rule of num_leaves_//1 makes no reference at all to the state, since the number of leaves is not modified when an inner node is processed.

Example query:

?- num_leaves(node(a,node(b,nil,nil),
                     node(c,nil,
                            node(d,nil,nil))), N).
N = 5.

The following nonterminals are useful for describing states with DCGs:

state(S), [S] --> [S].

state(S0, S), [S] --> [S0].

Note: Code in grey boxes may be useful for you to reuse in your own projects.

The nonterminal state(S) can be read as: "The current state is S". The nonterminal state(S0, S) can be read as: "The current state is S0, and henceforth it is S".

Using state//2, you can write num_leaves_//1 as:

num_leaves_(nil) --> state(N0, N), { N #= N0 + 1 }.
num_leaves_(node(_,Left,Right)) -->
        num_leaves_(Left),
        num_leaves_(Right).

This approach is readily generalized to multiple states that are threaded through: You can for example use a term s(S1,S2,...,Sn) in such cases.

Reading from files

In Scryer Prolog, SICStus Prolog and SWI-Prolog, DCGs can be transparently applied to files using Ulrich Neumerkel's library(pio). When you need to process input from files, first write a DCG that describes the input. This lets you test the DCG in a pure way using phrase/2, and then apply the DCG to files too by simply using phrase_from_file/2 instead of phrase/2.

Video:

In our first example, we read a whole file to a list of characters. This is very easy to do with seq//1 as defined above. For example, to read the contents of the file dcg.html to a list of characters, we use:

?- phrase_from_file(seq(Chars), "dcg.html").
   Chars = "<!DOCTYPE html>\n<ht ..."
;  false.

As another example, consider the following DCG that uses seq//1 to refer to a subsequence of characters:

like(What) --> "I like ", seq(What), ".", ... .

As before, we can use this DCG to parse a given list of characters:

?- phrase(like(What), "I like it. Anything can follow!").
   What = "it"
;  false.

As expected, What is unified with the atoms i and t.

Moreover, using library(pio) and its phrase_from_file/2, we can transparently parse from a file with the same DCG. Assume that the file like.txt starts with the string "I like it."

?- phrase_from_file(like(What), "like.txt").
   What = "it"
;  false.

Again, What is unified with the atoms i and t.

Pure input via library(pio) can be implemented in such a way that it uses memory efficiently when parsing files: First, the file can be read lazily, reading only as much as is needed. Second, file contents can be very compactly represented in memory if your Prolog system supports an efficient representation of lists of characters. Third, file contents that are no longer relevant for parsing can be reclaimed automatically if your Prolog system satisfies the properties outlined in Precise Garbage Collection in Prolog.

For these reasons, library(pio) is well-suited also for parsing large files.

Parsing tricks and techniques

When parsing, we often want to consume tokens greedily, meaning that the longest match should be given priority. We can do this by ordering the DCG rules accordingly. For example, the following DCG describes a list of whitespace characters in such a way that the longest such sequence is the first solution, using char_type/2 from library(charsio) for character classification:

ws --> [W], { char_type(W, whitespace) }, ws.
ws --> [].

Identifiers that must start with a letter and may contain either letters or digits can be parsed by applying this technique:

identifier([A|As]) --> [A], { char_type(A, alpha) }, symbol_r(As).

symbol_r([A|As]) --> [A], { char_type(A, alnum) }, symbol_r(As).
symbol_r([])     --> [].

As another technique that is sometimes useful for parsing, here are DCG rules that describe a list of lines that are terminated by line feed or end of file:

lines([])     --> call(eos), !.
lines([L|Ls]) --> line(L), lines(Ls).

line([])     --> ( "\n" | call(eos) ), !.
line([C|Cs]) --> [C], line(Cs).

eos([], []).

The nonterminal call//1 is used to call a Prolog predicate in such a way that the implicit DCG arguments are made available as explicit arguments. We need this to describe the condition "end of string". The grammar construct !//0 is used like the corresponding Prolog control structure.

We can use these definitions to obtain the contents of a file as a list of lines for further reasoning:

?- phrase_from_file(lines(Ls), "like.txt").
   Ls = ["I like it. Anythi ..."].

Note: eos/2 is comparatively rarely needed. In the above case it is used because anything else is the beginning of a new line. Typically, you can more directly express what you want to describe, and phrase/2 and phrase_from_file/2 only succeed if the complete list or file matches the description. Therefore, it is typically not necessary to explicitly refer to "end of the string".

Describing output

DCGs are also useful for describing output, because output is a list of characters. In library(format), Scryer Prolog provides the nonterminal format_//2 to declaratively describe output based on a format string that defines the layout of specified arguments.

Video:

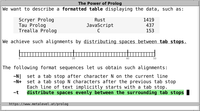
For example, we can describe a table with format_//2:

table -->
    row([this,is,a]),
    row([very,nice,table]).

row(Ls) --> format_("~t~w~7+~t~w~7+~t~w~7+~n", Ls).

Sample query and its results:

?- phrase(table, Ts).
   Ts = "   this     is      ...".

An important advantage of this declarative way to describe output is that we can write test cases and reason about it: It is quite hard to reason about output that only appears on the system terminal, with no other tangible manifestation. In contrast, it is easy to state properties that must hold about a list of characters.

When needed, we can show the table on the terminal with a single call of format/2:

?- phrase(table, Ts), format("~s", [Ts]).
   this     is      a
   very   nice  table
   Ts = "   this     is      ...".

Implementation

To see how DCGs are internally implemented in Scryer Prolog, we can use listing/1 from library(format). For example, to see the actual source code of num_leaves_//1, we declare the nonterminal dynamic via the dynamic/1 directive, and use:

?- listing(num_leaves_//1).
num_leaves_(nil,A,B) :-
   state(C,D,A,E),
   D#=C+1,
   E=B.
num_leaves_(node(A,B,C),D,E) :-
   num_leaves_(B,D,F),
   num_leaves_(C,F,E).

We see that internally, the two DCG rules of num_leaves_//1 were translated into Prolog rules with two additional arguments, following mechanical rewriting steps. The translation of DCGs to Prolog code is done by term_expansion/2, a mechanism analogous to macros in other languages.

For portability, it is best not to rely on a particular expansion method. Instead, use semicontext notation to refer to states and always use the phrase/[2,3] interface to invoke a DCG. This way, a Prolog system is free to apply a different expansion method that may be more efficient. For example, the last two arguments may as well be swapped and allow more efficient predicate calls this way due to specifics of a particular virtual machine.

Using DCGs

Consider using DCGs if you are:

describing a list
reading from a file
passing around a state representation that only a few predicates actually use or modify.

In every serious Prolog program, you will find many opportunities to use DCGs due to some subset of the above reasons.

Let us study one side-by-side comparison of a regular Prolog predicate and an equivalent DCG nonterminal to recall several important aspects of using DCGs and make some additional observations. We take the well-known Prolog predicate include/3 as an example:

regular Prolog

Prolog DCG

include(Goal, List, Included) :-
        include_(List, Goal, Included).

include_([], _, []).
include_([L|Ls], Goal, Included0) :-
        (   call(Goal, L) ->
            Included0 = [L|Included]
        ;   Included0 = Included
        ),
        include_(Ls, Goal, Included).

include(Goal, List, Included) :-
        phrase(include_(List, Goal), Included).

include_([], _) --> [].
include_([L|Ls], Goal) -->
        (   { call(Goal, L) } ->
            [L]
        ;   []
        ),
        include_(Ls, Goal).

Usage example for both versions:

?- include(integer, [a,b,c,1,2,e], Is).
Is = [1, 2].

We recall and note in particular:

phrase/2 must of course be used to refer to a DCG nonterminal within a regular Prolog predicate
conversely, {}//1 is used to call a regular Prolog goal within a DCG
the DCG version needs fewer explicit arguments, making it slightly easier to read and understand
although it is strongly related to the previous point, it is still worth mentioning explicitly that the DCG version also refers to fewer variables
using a DCG makes immediately clear that a list is being described.

Take your time and see for yourself which of the two versions you find easier to read and understand.

Some applications of DCGs that you can download from this site and study:

markov.pl uses DCGs to describe output of a Markov chain
Lisprolog uses DCGs to parse Lisp expressions and to implicitly thread through the state of the environment
Tist uses DCGs for all of the above reasons throughout the document
The comp.lang.prolog FAQ are described with a DCG.

Current developments

DCGs are currently being considered for inclusion in the Prolog ISO standard.

See ISO Prolog works by Ulrich Neumerkel for more information.

DCG notation is similar to monads which have been adopted as one of the most versatile among several competing formalisms in functional programming languages like Haskell. Other programming languages may also benefit from such constructs.

More about Prolog

Main page

Prolog DCG Primer

Introduction

Describing sequences with seq//1, seqq//1 and ... //0

List reversal, palindromes and other exercises

Relating trees to lists

Left recursion

Semicontext notation

Implicitly passing states around

Reading from files

Parsing tricks and techniques

Describing output

Implementation

Using DCGs

Current developments

Describing sequences with `seq//1`, `seqq//1` and `... //0`