Logical Foundations of Prolog
Logic is a very broad, interesting and also beautiful
topic.
| Video: |
|
There is no universally accepted definition for what logic
actually is. However, what we can say is that logic is
concerned—at least among other things—with the
properties of, and the relations between:
- syntax
This is the formalization of languages according to rules. It
includes for example defining what a formula or a sentence looks
like.
- semantics
This is assigning meaning to the
syntactic constructs of languages. This includes
defining how sentences are interpreted, and stating under what
conditions they are true.
- inferences
This stems from the Latin
verb inferre, which means "to carry forward". An
inference rule allows us to derive logical consequences
from premises, i.e., to bring premises to conclusions.
There are different logics, because changing these
components yields different frameworks.
Logic and computation are closely related. For example, we can
formulate logical statements about computations, and derive
logical consequences from them that correspond to results
of the computations.
It can be argued that programming is a form
of theory building. See
for example Programming
as Theory Building by Peter Naur.
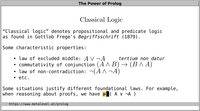
Prolog is based on classical first-order predicate logic.
| Video: |
|
In fact, the core of Prolog is restricted to a
Turing complete subset of first-order predicate logic
called Horn clauses.
| Video: |

|
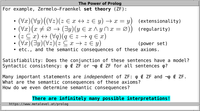
A Prolog program is a sequence of Horn clauses that define what is
true, and what follows from what.
Internally, Prolog uses a proof method
called resolution. Resolution
is based on the idea of proof by contradiction: To prove a logical
consequence of a set of axioms, we assume the opposite of what we
want to prove, and show that this contradicts the axioms which we
take for granted.
Logically, when Prolog answers a query, it tries to find
a resolution refutation of the negated query and the
set of clauses that constitute a program. When a refutation is
found, it means that the query, with the appropriate bindings, is
a logical consequence of the program.
For Horn clauses, resolution can be implemented very efficiently.
Resolution leaves a lot of freedom in how the search for
contradictions is to be performed. Accordingly, Prolog programs
can be interpreted with different evaluation strategies. The
default execution strategy is called SLDNF resolution:
SLD resolution with negation as finite failure.
Another popular execution strategy of Prolog programs is called
SLG resolution, also known
as tabling. Other
variants include iterative deepening and various heuristics.
Regarded as a theorem prover, Prolog with its default execution
strategy is incomplete in the sense that, in general,
not all logical consequences of a theory are found, because
infinite branches of the search tree may occlude them. For
example, even though a is a logical consequence of the
theory {a←a} ∪ {a}, a
depth-first traversal of the search space over admissible
inferences will not derive this if it gets caught up in the
infinite branch trying to derive a
from a←a by deriving a,
then again trying to derive a
from a←a etc.
Even though Prolog itself is incomplete in general, we can use it
to implement complete theorem
provers. This is because Prolog is a programming
language and can be used to express all known computations. In
addition, we can interpret Prolog programs with variants of
resolution that are themselves complete.
Since Prolog allows us to decouple the logical description
of what holds (i.e., the Horn clauses) from how the
search for logical consequences is performed, we can
write
Algorithm = Logic + Control.
More about Prolog
Main page



